Prezados,
O filme abaixo conta a história de um matemático indiano chamado Srinivasa Ramanujan (1887-1920), o gênio hindu do século vinte, que tinha a mesma incrível habilidade manipulativa em aritmética e álgebra que se encontra em Bhaskara. O matemático inglês G.H. Hardy uma vez visitou Ramanujan num hospital em Putney e mencionou a seu amigo que viera em um táxi com o número desinteressante 1729, e Ramanujan imediatamente observa que esse número ao contrário é interessante, pois é o menor inteiro que pode ser representado de dois modos diferentes como a soma de dois cubos 12 + 123= 1728= 93+103. Na obra de Ramanujan também observamos o caráter desorganizado, a força do raciocínio intuitivo, e pouco caso pela geometria que eram tão evidentes em seus predecessores.
Faça o download pelo torrent no link abaixo:
O homem que viu o infinito (Torrent)
Atenciosamente,
Professor Alexandre.
Este blog é destinado a todos os alunos do ensino fundamental e médio, e em especial para os meus alunos.
segunda-feira, 26 de setembro de 2016
quarta-feira, 14 de setembro de 2016
Exercícios de Recuperação (3.º anos do E.M.)
Prezados alunos,
Segue o link para download do exercício de recuperação que deve ser enviado pelo e-mail abaixo até dia 24/09. Não aceitarei posteriormente.
Não esqueça de colocar seu nome, número e série no email.
A atividade é individual.
E-mail: professor_alexandre@aseeducacional.com.br .
Link da atividade : Lista de Exercícios de Recuperação do 3.º ano do E.M. .
Segue o link para download do exercício de recuperação que deve ser enviado pelo e-mail abaixo até dia 24/09. Não aceitarei posteriormente.
Não esqueça de colocar seu nome, número e série no email.
A atividade é individual.
E-mail: professor_alexandre@aseeducacional.com.br .
Link da atividade : Lista de Exercícios de Recuperação do 3.º ano do E.M. .
Exercícios de Recuperação (2.º anos do E.M.)
Prezados alunos,
Segue o link para download do exercício de recuperação que deve ser enviado pelo e-mail abaixo até dia 24/09. Não aceitarei posteriormente.
Não esqueça de colocar seu nome, número e série no email.
A atividade é individual.
E-mail: professor_alexandre@aseeducacional.com.br .
Link da atividade: Lista de Exercícios de Recuperação (2.º ano do E.M.) .
Segue o link para download do exercício de recuperação que deve ser enviado pelo e-mail abaixo até dia 24/09. Não aceitarei posteriormente.
Não esqueça de colocar seu nome, número e série no email.
A atividade é individual.
E-mail: professor_alexandre@aseeducacional.com.br .
Link da atividade: Lista de Exercícios de Recuperação (2.º ano do E.M.) .
quarta-feira, 24 de agosto de 2016
Para 8.º séries (9.º anos)
Prezados Alunos,
Segue um exemplo de como fazer um gráfico no Excel. Este exemplo é uma função Afim. Baixar neste link Função Afim no Excel .
Atenciosamente,
Prof. Alexandre.
Segue um exemplo de como fazer um gráfico no Excel. Este exemplo é uma função Afim. Baixar neste link Função Afim no Excel .
Atenciosamente,
Prof. Alexandre.
Para 8.º séries (9.º anos)
Prezados alunos,
Segue abaixo o link de um software para fazer gráfico. Somente digitar a função no campo entrada que fica localizado na parte de baixo do software.
Exemplos:
F(x) = 2x ==> Digitamos no campo entrada y=2*x
F(x) = 4x-2 ==> Digitamos no campo entrada y=4*x-2
F(x) = x² -6x + 4 ==> Digitamos no campo entrada y=x^2-6*x+4
Link para baixar o Geogebra .
Atenciosamente,
Prof. Alexandre.
Segue abaixo o link de um software para fazer gráfico. Somente digitar a função no campo entrada que fica localizado na parte de baixo do software.
Exemplos:
F(x) = 2x ==> Digitamos no campo entrada y=2*x
F(x) = 4x-2 ==> Digitamos no campo entrada y=4*x-2
F(x) = x² -6x + 4 ==> Digitamos no campo entrada y=x^2-6*x+4
Link para baixar o Geogebra .
Atenciosamente,
Prof. Alexandre.
Para 8.º séries (9.º anos)
Prezados Alunos,
Segue um exemplo de como fazer um gráfico no Excel. Este exemplo é uma função linear. Baixar neste link Função Linear no Excel .
Atenciosamente,
Prof. Alexandre.
Segue um exemplo de como fazer um gráfico no Excel. Este exemplo é uma função linear. Baixar neste link Função Linear no Excel .
Atenciosamente,
Prof. Alexandre.
Para 8.º séries (9.º anos)
Caros Alunos,
Segue alguns desenhos no plano cartesiano. Plote os pontos e descobrirá o desenho.
Click no link https://docs.google.com/file/d/0B7DeV8K6VL-uVjFnTjlwYVlKTzQ/edit?pli=1 para baixar e depois imprima as folhas com o plano cartesiano e os pontos.
Atenciosamente,
Professor Alexandre.
Segue alguns desenhos no plano cartesiano. Plote os pontos e descobrirá o desenho.
Click no link https://docs.google.com/file/d/0B7DeV8K6VL-uVjFnTjlwYVlKTzQ/edit?pli=1 para baixar e depois imprima as folhas com o plano cartesiano e os pontos.
Atenciosamente,
Professor Alexandre.
sexta-feira, 19 de agosto de 2016
Para 8.º séries (9.º anos)
Caros Alunos,
Segue abaixo o link do papel milimetrado para download.
Papel Milimetrado .
Grato,
Professor Alexandre.
Segue abaixo o link do papel milimetrado para download.
Papel Milimetrado .
Grato,
Professor Alexandre.
segunda-feira, 13 de junho de 2016
Lista de Recuperação do 2.º Bimestre das 8.º séries / 9.º anos
Prezados alunos,
Segue a lista com os exercícios para recuperação de notas, data da entrega: 20/06/16.
O link da atividade: Lista de Exercícios de Recuperação do 2.º bimestre .
Grato,
Professor Alexandre.
Segue a lista com os exercícios para recuperação de notas, data da entrega: 20/06/16.
O link da atividade: Lista de Exercícios de Recuperação do 2.º bimestre .
Grato,
Professor Alexandre.
quinta-feira, 2 de junho de 2016
Alunos do Ensino Médio
Prezados alunos,
Segue abaixo um link de uma plataforma de videoaulas gratuitas com intuito de preparar os alunos ou demais interessados para a prova do ENEM que acontecerá em Novembro.
O conteúdo está classificado em Ciências da Natureza e suas Tecnologias; Linguagens, Códigos e suas Tecnologias; Matemática e suas Tecnologias; e Ciências Humanas e suas Tecnologias. Dá para fazer anotações, criar playlists com os seus vídeos prediletos, e o melhor, compartilhar tudo com a sua turma!
Plataforma de estudo para o ENEM (MECFLIX)
Grato,
Professor Alexandre.
Segue abaixo um link de uma plataforma de videoaulas gratuitas com intuito de preparar os alunos ou demais interessados para a prova do ENEM que acontecerá em Novembro.
O conteúdo está classificado em Ciências da Natureza e suas Tecnologias; Linguagens, Códigos e suas Tecnologias; Matemática e suas Tecnologias; e Ciências Humanas e suas Tecnologias. Dá para fazer anotações, criar playlists com os seus vídeos prediletos, e o melhor, compartilhar tudo com a sua turma!
Plataforma de estudo para o ENEM (MECFLIX)
Grato,
Professor Alexandre.
terça-feira, 17 de maio de 2016
Lista de Exercícios (3.º anos do E.M.)
Prezados alunos,
Seguem em dois formatos a lista de exercícios para entrega no dia 30/05, referente aos seguintes conteúdos: equação geral da reta e equação reduzida da reta.
Lista de Exercícios 2 (em Word)
Lista de Exercícios 2 (em PDF)
Atenciosamente,
Prof. Alexandre.
Seguem em dois formatos a lista de exercícios para entrega no dia 30/05, referente aos seguintes conteúdos: equação geral da reta e equação reduzida da reta.
Lista de Exercícios 2 (em Word)
Lista de Exercícios 2 (em PDF)
Atenciosamente,
Prof. Alexandre.
Equação geral e reduzida da reta (3.º anos)
Equação geral e reduzida da reta - resumo (com questões)
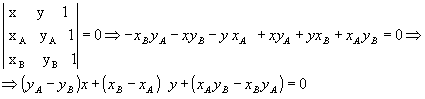
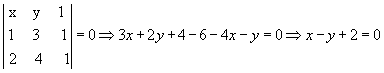
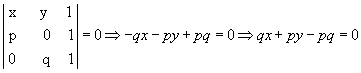
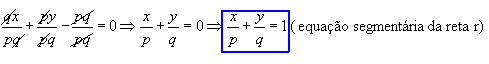
y = ax +b

A forma geral da equação reduzida da reta é dada pela expressão: y = ax + b. Utilizando o ponto P1(2, 7), temos:
y = ax + b
7 = a * 2 + b
2a + b = 7
Utilizando o ponto P2(–1, –5), temos:
–5 = a * (–1) + b
–5 = –a + b
–a + b = –5
Resolvendo o sistema, , determinamos o coeficiente angular e o linear.
, determinamos o coeficiente angular e o linear.


Aplicando Sarrus: produto dos termos da diagonal principal subtraído do produto dos termos da diagonal secundária.

Retas perpendiculares
Sabemos da Geometria Plana que duas retas são perpendiculares quando são concorrentes e formam entre si um ângulo reto (90º) . Sejam as retas r: y = mr x + nr e s: y = ms x + ns . Nestas condições podemos escrever a seguinte relação entre os seus coeficientes angulares:
ms = - 1 / mr ou mr . ms = -1 .
Dizemos então que se duas retas são perpendiculares, o produto dos seus coeficientes angulares
é igual a -1.
Exemplo:
Dadas as retas de equações (2w - 2)x + (w - 1)y + w = 0 e (w - 3)y + x - 2w = 0, podemos afirmar que:
a) elas são perpendiculares para qualquer valor de w
b) elas são perpendiculares se w = 1
c) elas são perpendiculares se w = -1
d) elas são perpendiculares se w = 0
e) essas retas não podem ser perpendiculares
Solução:
Podemos escrever para a 1ª reta: y = [-(2w-2) / (w-1)].x - w /(w-1).
Analogamente para a 2ª reta: y = [-1 / (w-3)].x + 2w / (w-3). Ora, os coeficientes de x são os coeficientes angulares e, pelo que já sabemos, a condição de perpendicularidade é que o produto desses coeficientes angulares seja igual a -1. Logo:

Efetuando os cálculos indicados e simplificando-se obtemos: w2 - 2w + 1 = 0, que é equivalente a
(w - 1)2 = 0, de onde conclui-se que w = 1.
Mas, cuidado! Observe que 1 anula o denominador da expressão acima e, portanto é uma raiz estranha, já que não existe divisão por zero! Apesar das aparências, a raiz 1 não serve! Logo, a alternativa correta é a letra E e não a letra B como ficou aparente.
Questões resolvidas sobre equação geral e reduzida da reta e retas perpendiculares
1) Determine a equação reduzida da reta t que forma um ângulo de 135o com o eixo das abscissas e que passa pelo ponto P(4, 5).
Solução:
y = -6t - 21
Qual a equação segmentária dessa trajetória?
Solução:
Multiplicando ambos os membros da 1ª equação paramétrica por 2, vem: 2x = 6t + 22. Somando agora membro a membro com a 2ª equação, obtemos: 2x + y = 32 (observe que a variável t é eliminada nessa operação pois 6t + ( -6t ) = 0 ). Dividindo ambos os membros da equação obtida por 32 fica:
2x / 32 + y / 32 = 32 / 32 \ x / 16 + y / 32 = 1, que é a equação segmentária procurada.
6) Determine a equação geral da reta sabendo que os pontos A(2,1) e B(- 2,4) pertencem a reta.
Solução:
Com dois pontos podemos determinar a equação da reta:
y = ax + b
*1 = 2a + b
*4 = -2a + b (+)
5 = b
2a + b = 1
2a + 5 = 1
2a = - 4
a = - 2
Logo a equação da reta é y = - 2x + 5, passando para a forma de equação geral fica:
2x + y - 5 = 0
7) A reta r é perpendicular à reta s. Sabendo-se que a reta s possui o seu coeficiente ângular igual à 1/2 e que a reta r passa pelo ponto A(5,3), determine a equação geral da reta r.
Y = - 4X / 5 + b <~~~~coeficiente angular igual a - 4/5
 11) Encontre a equação da reta s, perpendicular à reta t: 2x + 3y – 4 =0, sabendo que ela passa pelo ponto P(3,4).
11) Encontre a equação da reta s, perpendicular à reta t: 2x + 3y – 4 =0, sabendo que ela passa pelo ponto P(3,4).
Solução:

12) Prove que as retas s: x + 2y – 1 = 0 e r: 4x – 2y +12 = 0 são perpendiculares.
Solução:

13) (UFSC) De acordo com o gráfico abaixo, assinale a(s)
proposição(ões) VERDADEIRA(S).
Solução:
01 – Conforme o gráfico, a reta s intercepta o eixo x no ponto -2, então já temos um ponto, que é (-2,0).
O outro ponto é (0,3), pois é onde a reta corta o eixo y.
Preposição verdadeira
02 – Para que as retas sejam perpendiculares, seus coeficientes angulares devem ser opostos e inversos.
Na reta r devemos encontrar a equação reduzida, sabemos que ela é representada por:
Sabemos pelo gráfico que quando x é 0 y é 1, portanto:
Portanto:
Quando y = 0, x = 1. Logo:
Como a é -1, esse é o coeficiente angular da reta.
04 – Para que as retas interceptem-se no ponto x=4/5, lembra que abscissa é x, abXissa, aplicando esse ponto em x na equação reduzida das retas, y deve ter o mesmo valor nas duas:
Reta s
Reta r
Ítem falso
Substituindo y pelo seu valor na primeira reta:
O ponto é (1/5, 4/5) e a área será:
Falso
Soma dos ítens verdadeiros: 01
14) (UDESC 2008) A soma do coeficiente angular com o coeficiente linear da reta que passa pelos pontos A(1, 5) e B(4, 14) é:
a) 4
b) -5
c) 3
d) 2
e) 5
15) (ADVISE 2009) A equação geral da reta tangente à curva y = x² + x no ponto de abscissa 1 é:
a) 3x – y – 1 = 0
b) 3x – y = 0
c) 2x – y – 1 = 0
d) 2x – y = 0
e) 5x – 2y – 2 = 0
16) (USP) A equação da reta perpendicular ao eixo das abscissas que passa pelo ponto médio do segmento AB, onde A(2, 3) e B é o centro da circunferência de equação x2 + y2 - 8x - 6y + 24 = 0, é:
a) y = 3
b) y = 4
c) x = 4
d) x = 3
e) 3x + 4y = 0
Equação geral da reta
Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos.
Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos de r e P(x,y) um ponto genérico, também de r, estando A, B e P alinhados, podemos escrever:
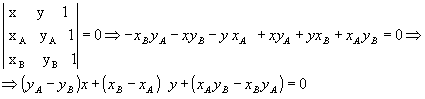
Fazendo yA - yB = a, xB - xA = b e xAyB - xByA=c, como a e b não são simultaneamente nulos 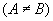 , temos:
, temos:
ax + by + c = 0
|
(equação geral da reta r)
Essa equação relaciona x e y para qualquer ponto P genérico da reta. Assim, dado o ponto P(m, n):
- se am + bn + c = 0, P é o ponto da reta;
- se am + bn + c
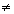 0, P não é ponto da reta.
0, P não é ponto da reta.
Acompanhe os exemplos:
- Vamos considerar a equação geral da reta r que passa por A(1, 3) e B(2, 4).
Considerando um ponto P(x, y) da reta, temos:
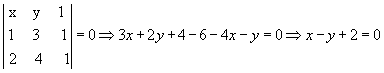
- Vamos verificar se os pontos P(-3, -1) e Q(1, 2) pertencem à reta r do exemplo anterior. Substituindo as coordenadas de P em x - y + 2 = 0, temos:
-3 - (-1) + 2 = 0 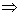 -3 + 1 + 2 = 0
-3 + 1 + 2 = 0
Como a igualdade é verdadeira, então P 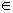 r.
r.
Substituindo as coordenadas de Q em x - y + 2 = 0, obtemos:
1 - 2 + 2 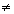 0
0
Como a igualdade não é verdadeira, então Q 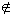 r.
r.
Equação segmentária
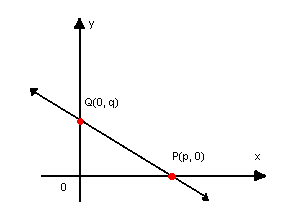
Considere a reta r não paralela a nenhum dos eixos e que intercepta os eixos nos pontos P(p, 0) e Q(0, q), com 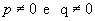 :
:

A equação geral de r é dada por:
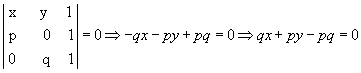
Dividindo essa equação por pq 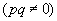 , temos:
, temos:
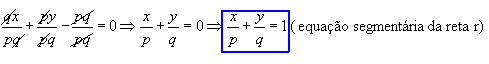
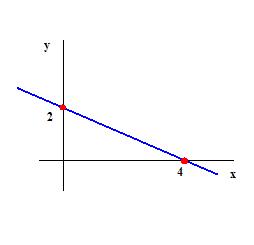
Como exemplo, vamos determinar a equação segmentária da reta que passa por P(3, 0) e Q(0, 2), conforme o gráfico:
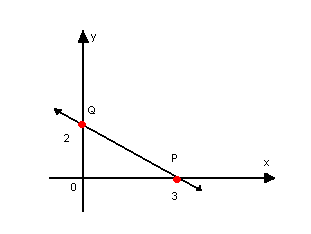 | 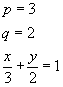 |
Exemplo: Determine a equação segmentária da reta t: 7x + 14y – 28 =0 e as coordenadas dos pontos de interseção da reta com os eixos do plano.
Solução:
Solução:
Para determinar a forma segmentária da equação da reta t devemos isolar o termo independente c. Assim, teremos:
7x + 14y = 28
Dividindo toda igualdade por 28, obtemos:
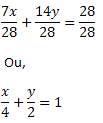
Que é a equação segmentária da reta t.
Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:
(4, 0) é o ponto de interseção da reta com o eixo x.
(0, 2) é o ponto de interseção da reta com o eixo y.
7x + 14y = 28
Dividindo toda igualdade por 28, obtemos:
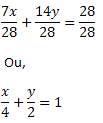
Que é a equação segmentária da reta t.
Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:
(4, 0) é o ponto de interseção da reta com o eixo x.
(0, 2) é o ponto de interseção da reta com o eixo y.
Equação reduzida da reta
Podemos representar uma reta no plano cartesiano por meio da condição geométrica ou por uma equação matemática. Em relação à equação matemática, a reta pode ser escrita nas seguintes formas: reduzida, segmentária, geral ou paramétrica. Vamos abordar a representação de uma equação reduzida de reta, demonstrando três possíveis situações.
Vamos considerar a equação da reta que passa por um ponto Q (x1, y1), com coeficiente angular a, observe:
y – y1 = a * (x – x1)
Escolhendo ao acaso, o ponto (0, b) e determinando que a reta o intersecte, temos que:
y – b = a * (x – 0)
y – b = a * x – a * 0
y – b = ax
y = ax + b
Portanto, a equação reduzida da reta possui a seguinte lei de formação:
Vamos considerar a equação da reta que passa por um ponto Q (x1, y1), com coeficiente angular a, observe:
y – y1 = a * (x – x1)
Escolhendo ao acaso, o ponto (0, b) e determinando que a reta o intersecte, temos que:
y – b = a * (x – 0)
y – b = a * x – a * 0
y – b = ax
y = ax + b
Portanto, a equação reduzida da reta possui a seguinte lei de formação:
y = ax +b
Exemplo 1:
Utilizando o ponto P1(2, 7), no qual x = 2 e y = 7, temos:
y – y1 = a * (x – x1)
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8
y = 4x – 8 + 7
y = 4x – 1
Exemplo 2:
Utilizando o ponto P1(2, 7), no qual x = 2 e y = 7, temos:
y – y1 = a * (x – x1)
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8
y = 4x – 8 + 7
y = 4x – 1
Exemplo 2:
A forma geral da equação reduzida da reta é dada pela expressão: y = ax + b. Utilizando o ponto P1(2, 7), temos:
y = ax + b
7 = a * 2 + b
2a + b = 7
Utilizando o ponto P2(–1, –5), temos:
–5 = a * (–1) + b
–5 = –a + b
–a + b = –5
Resolvendo o sistema,
Substituindo os valores de a e b na expressão matemática, temos:
y = ax + b
y = 4x – 1
Exemplo 3:
Podemos construir uma matriz quadrada com os pontos fornecidos e um ponto genérico (x, y). O determinante dessa matriz será a equação da reta. Observe:
P1(2, 7) e P2(–1, –5)
y = ax + b
y = 4x – 1
Exemplo 3:
Podemos construir uma matriz quadrada com os pontos fornecidos e um ponto genérico (x, y). O determinante dessa matriz será a equação da reta. Observe:
P1(2, 7) e P2(–1, –5)
Aplicando Sarrus: produto dos termos da diagonal principal subtraído do produto dos termos da diagonal secundária.
[(x * 7 * 1) + (–1 * 1 * y) + (–5 * 2 * 1)] – [(–1 * 7 * 1) + (y * 2 * 1) + (–5 * x * 1)] = 0
[7x – y –10] – [–7 + 2y – 5x] = 0
7x – y – 10 + 7 – 2y + 5x = 0
12x – 3y – 3 = 0
–3y = –12x + 3 (dividir todos por – 3)
y = 4x – 1
[7x – y –10] – [–7 + 2y – 5x] = 0
7x – y – 10 + 7 – 2y + 5x = 0
12x – 3y – 3 = 0
–3y = –12x + 3 (dividir todos por – 3)
y = 4x – 1
Retas perpendiculares
Sabemos da Geometria Plana que duas retas são perpendiculares quando são concorrentes e formam entre si um ângulo reto (90º) . Sejam as retas r: y = mr x + nr e s: y = ms x + ns . Nestas condições podemos escrever a seguinte relação entre os seus coeficientes angulares:
ms = - 1 / mr ou mr . ms = -1 .
Dizemos então que se duas retas são perpendiculares, o produto dos seus coeficientes angulares
é igual a -1.
Exemplo:
Dadas as retas de equações (2w - 2)x + (w - 1)y + w = 0 e (w - 3)y + x - 2w = 0, podemos afirmar que:
a) elas são perpendiculares para qualquer valor de w
b) elas são perpendiculares se w = 1
c) elas são perpendiculares se w = -1
d) elas são perpendiculares se w = 0
e) essas retas não podem ser perpendiculares
Solução:
Podemos escrever para a 1ª reta: y = [-(2w-2) / (w-1)].x - w /(w-1).
Analogamente para a 2ª reta: y = [-1 / (w-3)].x + 2w / (w-3). Ora, os coeficientes de x são os coeficientes angulares e, pelo que já sabemos, a condição de perpendicularidade é que o produto desses coeficientes angulares seja igual a -1. Logo:
Efetuando os cálculos indicados e simplificando-se obtemos: w2 - 2w + 1 = 0, que é equivalente a
(w - 1)2 = 0, de onde conclui-se que w = 1.
Mas, cuidado! Observe que 1 anula o denominador da expressão acima e, portanto é uma raiz estranha, já que não existe divisão por zero! Apesar das aparências, a raiz 1 não serve! Logo, a alternativa correta é a letra E e não a letra B como ficou aparente.
Fontes: www.mundoeducacao.com.br
Questões resolvidas sobre equação geral e reduzida da reta e retas perpendiculares
1) Determine a equação reduzida da reta t que forma um ângulo de 135o com o eixo das abscissas e que passa pelo ponto P(4, 5).
Sabemos que α = 135o e que a equação reduzida da reta é da forma y = mx + q. Assim, temos que:
m = tg 135o = – 1
Como a reta t passa pelo ponto P, obtemos:
5 = -1*4 + q
q = 5 + 4 = 9
Portanto, a equação reduzida da reta t é y = – x + 9.
2) Determine a equação reduzida da reta s que passa pelos pontos A(1, 0) e B(3, 4).
m = tg 135o = – 1
Como a reta t passa pelo ponto P, obtemos:
5 = -1*4 + q
q = 5 + 4 = 9
Portanto, a equação reduzida da reta t é y = – x + 9.
2) Determine a equação reduzida da reta s que passa pelos pontos A(1, 0) e B(3, 4).
Solução:
Como conhecemos dois pontos da reta s, podemos encontrar sua equação geral.
Desenvolvendo o determinante obtemos:
2y – 4x + 4 = 0
Isolando y teremos:

Ou
y = 2x – 2
Desenvolvendo o determinante obtemos:
2y – 4x + 4 = 0
Isolando y teremos:
Ou
y = 2x – 2
3) Calcule o coeficiente angular das retas de equações:
a) 3x + 4y - 7 = 0
b) -6x + 8y + 3 = 0
Solução:
a) 4y = -3x + 7
y = -3 x + 7 coeficiente angular = -3
4 4 4
b) 8y = 6x - 3
y = 6 x - 3 = 3 x - 3 coeficiente angular = 3
8 8 4 8 4
4) Ache a equação segmentária da reta de equação geral 2x + 3y - 18 = 0.
Solução:
Podemos escrever: 2x + 3y = 18 ; dividindo ambos os membros por 18 vem:
2x/18 + 3y/18 = 18/18 \ x / 9 + y / 6 = 1.
Vemos, portanto que p = 9 e q = 6 e portanto a reta corta os eixos coordenados nos pontos A(9,0) e B(0,6).
5) Um móvel descreve uma trajetória retilínea e suas coordenadas em função do tempo t , são:
x = 3t + 11y = -6t - 21
Qual a equação segmentária dessa trajetória?
Solução:
Multiplicando ambos os membros da 1ª equação paramétrica por 2, vem: 2x = 6t + 22. Somando agora membro a membro com a 2ª equação, obtemos: 2x + y = 32 (observe que a variável t é eliminada nessa operação pois 6t + ( -6t ) = 0 ). Dividindo ambos os membros da equação obtida por 32 fica:
2x / 32 + y / 32 = 32 / 32 \ x / 16 + y / 32 = 1, que é a equação segmentária procurada.
6) Determine a equação geral da reta sabendo que os pontos A(2,1) e B(- 2,4) pertencem a reta.
Solução:
Com dois pontos podemos determinar a equação da reta:
y = ax + b
*1 = 2a + b
*4 = -2a + b (+)
5 = b
2a + b = 1
2a + 5 = 1
2a = - 4
a = - 2
Logo a equação da reta é y = - 2x + 5, passando para a forma de equação geral fica:
2x + y - 5 = 0
7) A reta r é perpendicular à reta s. Sabendo-se que a reta s possui o seu coeficiente ângular igual à 1/2 e que a reta r passa pelo ponto A(5,3), determine a equação geral da reta r.
Solução:
Para determinarmos a equação geral da reta r, necessitaremos do seu coeficiente ângular e de um ponto. Como as retas r e s são perpendiculares, logo o produto de seus coeficientes é igual à -1.
mr * ms = - 1
mr * (1/2) = - 1
mr = - 2
Reta r : mr = - 2 ; A(5,3)
y - yo = m(x - xo)
y - 3 = - 2(x - 5)
y - 3 = - 2x + 10
y = - 2x + 13
2x + y - 13 = 0
Para determinarmos a equação geral da reta r, necessitaremos do seu coeficiente ângular e de um ponto. Como as retas r e s são perpendiculares, logo o produto de seus coeficientes é igual à -1.
mr * ms = - 1
mr * (1/2) = - 1
mr = - 2
Reta r : mr = - 2 ; A(5,3)
y - yo = m(x - xo)
y - 3 = - 2(x - 5)
y - 3 = - 2x + 10
y = - 2x + 13
2x + y - 13 = 0
8) Determine a equação da reta que passa pelo ponto P (-1, -2) e forma com os eixos coordenados um triângulo de área 4 u.a.
Solução:
Seja m o coeficiente angular da reta:
y - (-2) = m*[x - (-1) -----> y = mx + m - 2
Para x = 0 ----> y = m - 2
Para y = 0 ----> x = - (m - 2)/m
S = x*y ----> S = - [(m - 2)/m]*(m - 2)/2 ----> 4 = - (m - 2)²/2m ----> 8m = - (m - 2)² ----> 8m = - m² + 4m - 4 -----> m² + 4m + 4 = 0
Raiz dupla ----> m = - 2
Reta ----> y = - 2x - 2 - 2 -----> y = - 2x - 4
y - (-2) = m*[x - (-1) -----> y = mx + m - 2
Para x = 0 ----> y = m - 2
Para y = 0 ----> x = - (m - 2)/m
S = x*y ----> S = - [(m - 2)/m]*(m - 2)/2 ----> 4 = - (m - 2)²/2m ----> 8m = - (m - 2)² ----> 8m = - m² + 4m - 4 -----> m² + 4m + 4 = 0
Raiz dupla ----> m = - 2
Reta ----> y = - 2x - 2 - 2 -----> y = - 2x - 4
9) (PUC) Determine a equação da reta com coeficiente angular igual a - 4/5, e que passa pelo ponto p (2, -5).
Solução:
Y = - 4X / 5 + b <~~~~coeficiente angular igual a - 4/5
...que passa em (2,-5)...
-5 = - 4x2 / 5 + b
b = -5 + 8/5
b = (8-25) /5
b = - 17/5 <~~~~
............
Y = - 4X / 5 - 17/5
5Y = - 4X - 17
10) Considere no plano cartesiano uma reta r de equação 3x + 5y +1 =0 e um ponto Q de coordenadas (5,5). Determine a equação da resta s perpendicular a r passando por Q.
Solução:
Solução:
12) Prove que as retas s: x + 2y – 1 = 0 e r: 4x – 2y +12 = 0 são perpendiculares.
Solução:
13) (UFSC) De acordo com o gráfico abaixo, assinale a(s)
proposição(ões) VERDADEIRA(S).
01. A equação da reta s é 3x – 2y + 6 = 0.
02. A reta s e a reta r são perpendiculares.
04. As retas r e s se interceptam no ponto de abscissa 4/5.
08. A área da região do plano limitada pelas retas r, s e pelo eixo das abscissas é igual a 3/10 unidades área.
Solução:
01 – Conforme o gráfico, a reta s intercepta o eixo x no ponto -2, então já temos um ponto, que é (-2,0).
O outro ponto é (0,3), pois é onde a reta corta o eixo y.
Com esses dois pontos fica fácil obter a equação da reta com os dois pontos e um terceiro (x,y) sendo a área desses ponto igual a zero, para que seja uma reta:
|0 -2 x 0| = 0
|3 0 y 3 |
-2y+3x+6 = 0
Preposição verdadeira
02 – Para que as retas sejam perpendiculares, seus coeficientes angulares devem ser opostos e inversos.
Para obter o coeficiente angular, devemos observar a equação reduzida das duas retas, vejamos na reta s:
-2y+3x+6 = 0
2y = 3x+6
y = 3x+3
2
O coeficiente angular será 3/2, o coeficiente de x.
Na reta r devemos encontrar a equação reduzida, sabemos que ela é representada por:
y = ax+b
Sabemos pelo gráfico que quando x é 0 y é 1, portanto:
1 = 0.a+b
b = 1
Portanto:
y = ax+1
Quando y = 0, x = 1. Logo:
0 = a.1+1
a = -1
Como a é -1, esse é o coeficiente angular da reta.
Com -1 e 3/2 não temos oposto nem inverso.
Ítem falso
04 – Para que as retas interceptem-se no ponto x=4/5, lembra que abscissa é x, abXissa, aplicando esse ponto em x na equação reduzida das retas, y deve ter o mesmo valor nas duas:
Reta s
y = 3x+3
2
y = 3. 4 + 3
2 5
y = 12 + 1
10
y = 22
10
y = 11
5
Reta r
y = -x+1
y = -4 + 1
5
y = 1
5
Ítem falso
08 – Será a área por coordenadas entre os pontos (-2, 0); (1,0) e o ponto de intersecção das duas retas, que é o ponto comum entre as duas, para achar esse ponto, resolvemos as duas equações de reta como um sistema linear, achando x e y que é comum aos dois:
y = 3x+3 y = -x+1
2
y = -x+1
Substituindo y pelo seu valor na primeira reta:
3x+3 = -x+1
2
-2x+2 = 3x+3
5x = 1
x = 1/5
y = -x+1
y = -1+1
5
y = 4/5
O ponto é (1/5, 4/5) e a área será:
A = 1/2|-2 1 1/5 -2|
| 0 0 4/5 0|
A = 1/2 |4/5+8/5|
A = 1/2. 12/5
A = 12/10
A = 6/5
Falso
Soma dos ítens verdadeiros: 01
14) (UDESC 2008) A soma do coeficiente angular com o coeficiente linear da reta que passa pelos pontos A(1, 5) e B(4, 14) é:
a) 4
b) -5
c) 3
d) 2
e) 5
15) (ADVISE 2009) A equação geral da reta tangente à curva y = x² + x no ponto de abscissa 1 é:
a) 3x – y – 1 = 0
b) 3x – y = 0
c) 2x – y – 1 = 0
d) 2x – y = 0
e) 5x – 2y – 2 = 0
16) (USP) A equação da reta perpendicular ao eixo das abscissas que passa pelo ponto médio do segmento AB, onde A(2, 3) e B é o centro da circunferência de equação x2 + y2 - 8x - 6y + 24 = 0, é:
a) y = 3
b) y = 4
c) x = 4
d) x = 3
e) 3x + 4y = 0
17) Determinar as equações das retas (t) tangentes à circunferência x² + y² + 2x - 3 = 0 e que passam pelo ponto P(5, 2). Resp: y - 2 = 0 e 3x - 4y - 7 = 0
segunda-feira, 16 de maio de 2016
Estudo da Reta (Geometria Analítica) 3.º anos do E.M.
Prezados alunos,
Segue no documento para download, um pouco mais de explicação sobre retas em geometria analítica.
Estudo da Reta
Atenciosamente,
Professor Alexandre.
Segue no documento para download, um pouco mais de explicação sobre retas em geometria analítica.
Estudo da Reta
Atenciosamente,
Professor Alexandre.
Lista de Exercícios para o 2.º C e D do E.M.
Prezados alunos,
Segue a lista de exercícios para entrega em 24/05/16. Pode ser feito em dupla.
Você pode escolher para fazer download entre os arquivos em word e pdf .
Lista de Exercícios II (Trigonometria) (Word) ;
Lista de Exercícios II (Trigonometria) (PDF) .
Segue a lista de exercícios para entrega em 24/05/16. Pode ser feito em dupla.
Você pode escolher para fazer download entre os arquivos em word e pdf .
Lista de Exercícios II (Trigonometria) (Word) ;
Lista de Exercícios II (Trigonometria) (PDF) .
Lista de Exercícios 9.º anos (8.º séries)
Prezados alunos,
Seguem as lista de exercícios para entrega dia 30/05. Os exercícios podem ser feitos em dupla.
Os exercícios estão em dois formatos, você pode escolher em word ou pdf.
Atenciosamente,
Prof. Alexandre.
domingo, 15 de maio de 2016
Para 8.º séries ==> Software chamado Raízes
Prezados,
Foi desenvolvido em linguagem C, o software chamado Raízes. Ele calcula todas as raízes.
O link está abaixo e na página softwares desenvolvidos pelo Prof. Alexandre.
Raízes .
Atenciosamente,
Prof. Alexandre.
Foi desenvolvido em linguagem C, o software chamado Raízes. Ele calcula todas as raízes.
O link está abaixo e na página softwares desenvolvidos pelo Prof. Alexandre.
Raízes .
Atenciosamente,
Prof. Alexandre.
quarta-feira, 11 de maio de 2016
Link do Basic256
Prezados,
Estou enviando mais um link do Basic256. Este link é direto do servidor.
Basic256
Atenciosamente,
Prof. Alexandre.
Estou enviando mais um link do Basic256. Este link é direto do servidor.
Basic256
Atenciosamente,
Prof. Alexandre.
segunda-feira, 9 de maio de 2016
ENEM 2016
Prezados,
As inscrições para o Enem (Exame Nacional do Ensino Médio) deste ano poderão ser realizadas a partir desta segunda-feira (9). Os interessados devem se inscrever exclusivamente pela internet, no site http://enem.inep.gov.br/participante. As inscrições terminam no dia 20 de maio, às 23h59.
Mais informações no link abaixo:
Informações ENEM .
As inscrições para o Enem (Exame Nacional do Ensino Médio) deste ano poderão ser realizadas a partir desta segunda-feira (9). Os interessados devem se inscrever exclusivamente pela internet, no site http://enem.inep.gov.br/participante. As inscrições terminam no dia 20 de maio, às 23h59.
Mais informações no link abaixo:
Informações ENEM .
domingo, 8 de maio de 2016
Linguagem Basic: Aula 3 - Operadores matemáticos
Prezados,
Na aula passada aprendemos o comando "input" que é usado para dar entrada em uma palavra ou número na memória do computador e o comando "print" que a saída da palavra ou número da memória para a tela.
Agora iremos aprender como fazemos programas de contas básicas, por exemplo soma, subtração, multiplicação, divisão e potenciação.
Os operadores matemáticos do Basic são:
+ ==> Soma
- ==> Subtração
* ==> Multiplicação
/ ==> Divisão
^ ==> Potenciação.
Um programa que calcula a adição de dois números, precisamos pedir dois números para efetuar o cálculo, então prosseguimos a seguinte forma:
input " Digite um Número", c
input "Digite outro Número", d
Agora precisamos processar e guardar este processamento em uma variável, então fazemos da seguinte maneira:
e= c + d
Depois do processamento, agora temos que mostrar o resultado na tela, então utilizamos o comando "print" que vimos na primeira aula. Tiramos o resultado já processado da variável "e".
print e
Seguem as telas de um programa de adição ou soma:

Na aula passada aprendemos o comando "input" que é usado para dar entrada em uma palavra ou número na memória do computador e o comando "print" que a saída da palavra ou número da memória para a tela.
Agora iremos aprender como fazemos programas de contas básicas, por exemplo soma, subtração, multiplicação, divisão e potenciação.
Os operadores matemáticos do Basic são:
+ ==> Soma
- ==> Subtração
* ==> Multiplicação
/ ==> Divisão
^ ==> Potenciação.
Um programa que calcula a adição de dois números, precisamos pedir dois números para efetuar o cálculo, então prosseguimos a seguinte forma:
input " Digite um Número", c
input "Digite outro Número", d
Agora precisamos processar e guardar este processamento em uma variável, então fazemos da seguinte maneira:
e= c + d
Depois do processamento, agora temos que mostrar o resultado na tela, então utilizamos o comando "print" que vimos na primeira aula. Tiramos o resultado já processado da variável "e".
print e
Seguem as telas de um programa de adição ou soma:

Um programa que calcula a subtração de dois números, precisamos pedir dois números para efetuar o cálculo, então prosseguimos a seguinte forma:
input " Digite um Número", c
input "Digite outro Número", d
Agora precisamos processar e guardar este processamento em uma variável, então fazemos da seguinte maneira:
e= c - d
Depois do processamento, agora temos que mostrar o resultado na tela, então utilizamos o comando "print" que vimos na primeira aula. Tiramos o resultado já processado da variável "e".
print e
Seguem as telas de um programa de subtração:
sábado, 7 de maio de 2016
Aula 2 - Linguagem programação Basic ==> Variáveis Númericas e Alfanuméricas
Prezados,
Na aula 1, fizemos o download da plataforma Basic256 e aprendemos como escrever na tela com o comando "print", usado na maioria das linguagens, com algumas alterações, por exemplo:
Agora vamos aprender o que são variáveis e quais são as variáveis mais importantes no uso da linguagem Basic.
As variáveis são divididas em dois tipos:
Exemplo:
As variáveis alfanuméricas são responsáveis por guardar as informações não numéricas na memória do computador. As variáveis alfanuméricas são simbolizados por uma letra, junção de letras ou palavras acrescentados de $.
Exemplo2:
Cuidado:
Agora com o entendimento das variáveis podemos aprender um novo comando do Basic256 e da linguagem Basic no geral.
Input: é a entrada de dados na memória do computador.
Exemplo: quero guardar na memória do computador um número qualquer, então procedemos da seguinte maneira:
input
input "digite um número", a ==> Estarei pedindo que digite um número e armazenando na variável "a".
print a ==> Imprime (escreve) na tela o número digitado.

Exemplo2: quero guardar na memória do computador a palavra laranja, então procedemos da seguinte maneira:
input "laranja", a$ ==> trata-se de uma palavra, então usamos as variáveis alfanuméricas. Será guardada na memória na posição a$.
ou
input "digite uma palavra", s$ ==> entrada de uma palavra , então usamos a variável alfanuméricas.
print s$ ==> imprime(escreve) na tela a palavra que você digitou na memória s$.
Este programinha pede uma palavra e depois imprime(escreve) na tela.
Agora faça você um programa que pede uma palavra e depois escreve a mesma na tela.
Até a próxima aula,
Prof. Alexandre.
Na aula 1, fizemos o download da plataforma Basic256 e aprendemos como escrever na tela com o comando "print", usado na maioria das linguagens, com algumas alterações, por exemplo:
- Na linguagem C, usamos o printf.
Agora vamos aprender o que são variáveis e quais são as variáveis mais importantes no uso da linguagem Basic.
As variáveis são divididas em dois tipos:
- Variáveis Numéricas;
- Variáveis Alfanuméricas.
Exemplo:
- a,b,c,...
- ab,ac,ad ou qualquer outra junção de letras.
- palavras quaisquer.
As variáveis alfanuméricas são responsáveis por guardar as informações não numéricas na memória do computador. As variáveis alfanuméricas são simbolizados por uma letra, junção de letras ou palavras acrescentados de $.
Exemplo2:
- a$, b$,...
- ab$, ac$ ou qualquer junção de letras acrescentado de $.
- palavras quaisquer acrescentado de $. Ex.: musica$, cadastro$, etc...
Cuidado:
- Não devemos utilizar as mesmas variáveis para palavras diferentes, pois estarei apagando a palavra anterior e acrescentado a palavra posterior.
Agora com o entendimento das variáveis podemos aprender um novo comando do Basic256 e da linguagem Basic no geral.
Input: é a entrada de dados na memória do computador.
Exemplo: quero guardar na memória do computador um número qualquer, então procedemos da seguinte maneira:
input
input "digite um número", a ==> Estarei pedindo que digite um número e armazenando na variável "a".
print a ==> Imprime (escreve) na tela o número digitado.

Exemplo2: quero guardar na memória do computador a palavra laranja, então procedemos da seguinte maneira:
input "laranja", a$ ==> trata-se de uma palavra, então usamos as variáveis alfanuméricas. Será guardada na memória na posição a$.
ou
input "digite uma palavra", s$ ==> entrada de uma palavra , então usamos a variável alfanuméricas.
print s$ ==> imprime(escreve) na tela a palavra que você digitou na memória s$.
Este programinha pede uma palavra e depois imprime(escreve) na tela.
Agora faça você um programa que pede uma palavra e depois escreve a mesma na tela.
Até a próxima aula,
Prof. Alexandre.
sexta-feira, 6 de maio de 2016
Geometria Analítica - 3.º anos do E.M.
Prezados,
Foi disponibilizado para download um software que calcula alguns dos principais itens da geometria analítica. Futuramente estarei atualizando com mais opções de cálculo da geometria analítica.
Ele está localizado em Software de Matemática /Estatística (Autor: Prof. Alexandre) com o nome de geometria analítica (item 9) .
O software foi desenvolvido pelo Prof. Alexandre em linguagem C.
Atenciosamente,
Prof. Alexandre.
Foi disponibilizado para download um software que calcula alguns dos principais itens da geometria analítica. Futuramente estarei atualizando com mais opções de cálculo da geometria analítica.
Ele está localizado em Software de Matemática /Estatística (Autor: Prof. Alexandre) com o nome de geometria analítica (item 9) .
O software foi desenvolvido pelo Prof. Alexandre em linguagem C.
Atenciosamente,
Prof. Alexandre.
Programação Basic
Prezados alunos,
Segue o link do basic256, uma linguagem básica para o aprendizado da lógica.
Basic 256 (Baixar e copiar todos os arquivos para a mesma pasta. Lembre-se que o arquivo .exe que deve ser executado para iniciar a plataforma Basic 256 ).
Basic 256 usa a antiga linguagem basic com muitos aprimoramentos.
Vou explicando aos poucos para um bom aprendizado.
Vamos começar com alguns comandos:
print ==> escreve na tela o que você quiser.
Ex: print "Meu Primeiro Programa"
Você vai no parte superior no ícone executar.
Irá aparecer do lado superior direito o que você pediu para escrever na tela.
Segue o link do basic256, uma linguagem básica para o aprendizado da lógica.
Basic 256 (Baixar e copiar todos os arquivos para a mesma pasta. Lembre-se que o arquivo .exe que deve ser executado para iniciar a plataforma Basic 256 ).
Basic 256 usa a antiga linguagem basic com muitos aprimoramentos.
Vou explicando aos poucos para um bom aprendizado.
Vamos começar com alguns comandos:
print ==> escreve na tela o que você quiser.
Ex: print "Meu Primeiro Programa"
Você vai no parte superior no ícone executar.
Irá aparecer do lado superior direito o que você pediu para escrever na tela.
Caso queira salvar, clique no ícone guardar, abrirá uma janela para você escolher onde vc quer salvar o programa . Ele salvará na extensão .kbs .
Até a próxima explicação.
Atenciosamente,
Prof. Alexandre.
Assinar:
Comentários (Atom)








