Equação geral da reta
Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos.
Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos de r e P(x,y) um ponto genérico, também de r, estando A, B e P alinhados, podemos escrever:
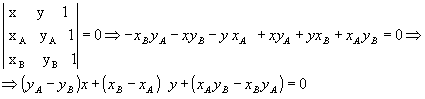
Fazendo yA - yB = a, xB - xA = b e xAyB - xByA=c, como a e b não são simultaneamente nulos 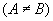 , temos:
, temos:
ax + by + c = 0
|
(equação geral da reta r)
Essa equação relaciona x e y para qualquer ponto P genérico da reta. Assim, dado o ponto P(m, n):
- se am + bn + c = 0, P é o ponto da reta;
- se am + bn + c
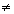 0, P não é ponto da reta.
0, P não é ponto da reta.
Acompanhe os exemplos:
- Vamos considerar a equação geral da reta r que passa por A(1, 3) e B(2, 4).
Considerando um ponto P(x, y) da reta, temos:
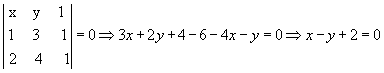
- Vamos verificar se os pontos P(-3, -1) e Q(1, 2) pertencem à reta r do exemplo anterior. Substituindo as coordenadas de P em x - y + 2 = 0, temos:
-3 - (-1) + 2 = 0 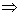 -3 + 1 + 2 = 0
-3 + 1 + 2 = 0
Como a igualdade é verdadeira, então P 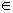 r.
r.
Substituindo as coordenadas de Q em x - y + 2 = 0, obtemos:
1 - 2 + 2 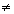 0
0
Como a igualdade não é verdadeira, então Q 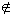 r.
r.
Equação segmentária
Considere a reta r não paralela a nenhum dos eixos e que intercepta os eixos nos pontos P(p, 0) e Q(0, q), com 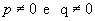 :
:
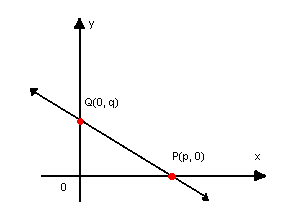
A equação geral de r é dada por:
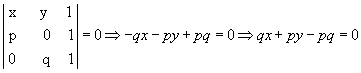
Dividindo essa equação por pq 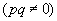 , temos:
, temos:
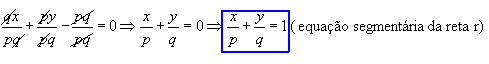
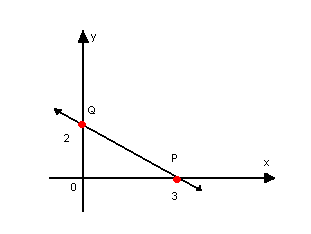
Como exemplo, vamos determinar a equação segmentária da reta que passa por P(3, 0) e Q(0, 2), conforme o gráfico:
 | 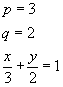 |
Exemplo: Determine a equação segmentária da reta t: 7x + 14y – 28 =0 e as coordenadas dos pontos de interseção da reta com os eixos do plano.
Solução:
Solução:
Para determinar a forma segmentária da equação da reta t devemos isolar o termo independente c. Assim, teremos:
7x + 14y = 28
Dividindo toda igualdade por 28, obtemos:
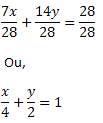
Que é a equação segmentária da reta t.
Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:
(4, 0) é o ponto de interseção da reta com o eixo x.
(0, 2) é o ponto de interseção da reta com o eixo y.
7x + 14y = 28
Dividindo toda igualdade por 28, obtemos:
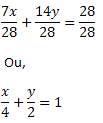
Que é a equação segmentária da reta t.
Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:
(4, 0) é o ponto de interseção da reta com o eixo x.
(0, 2) é o ponto de interseção da reta com o eixo y.
Equação reduzida da reta
Podemos representar uma reta no plano cartesiano por meio da condição geométrica ou por uma equação matemática. Em relação à equação matemática, a reta pode ser escrita nas seguintes formas: reduzida, segmentária, geral ou paramétrica. Vamos abordar a representação de uma equação reduzida de reta, demonstrando três possíveis situações.
Vamos considerar a equação da reta que passa por um ponto Q (x1, y1), com coeficiente angular a, observe:
y – y1 = a * (x – x1)
Escolhendo ao acaso, o ponto (0, b) e determinando que a reta o intersecte, temos que:
y – b = a * (x – 0)
y – b = a * x – a * 0
y – b = ax
y = ax + b
Portanto, a equação reduzida da reta possui a seguinte lei de formação:
Vamos considerar a equação da reta que passa por um ponto Q (x1, y1), com coeficiente angular a, observe:
y – y1 = a * (x – x1)
Escolhendo ao acaso, o ponto (0, b) e determinando que a reta o intersecte, temos que:
y – b = a * (x – 0)
y – b = a * x – a * 0
y – b = ax
y = ax + b
Portanto, a equação reduzida da reta possui a seguinte lei de formação:
y = ax +b
Exemplo 1:
Utilizando o ponto P1(2, 7), no qual x = 2 e y = 7, temos:
y – y1 = a * (x – x1)
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8
y = 4x – 8 + 7
y = 4x – 1
Exemplo 2:
Utilizando o ponto P1(2, 7), no qual x = 2 e y = 7, temos:
y – y1 = a * (x – x1)
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8
y = 4x – 8 + 7
y = 4x – 1
Exemplo 2:
A forma geral da equação reduzida da reta é dada pela expressão: y = ax + b. Utilizando o ponto P1(2, 7), temos:
y = ax + b
7 = a * 2 + b
2a + b = 7
Utilizando o ponto P2(–1, –5), temos:
–5 = a * (–1) + b
–5 = –a + b
–a + b = –5
Resolvendo o sistema,
Substituindo os valores de a e b na expressão matemática, temos:
y = ax + b
y = 4x – 1
Exemplo 3:
Podemos construir uma matriz quadrada com os pontos fornecidos e um ponto genérico (x, y). O determinante dessa matriz será a equação da reta. Observe:
P1(2, 7) e P2(–1, –5)
y = ax + b
y = 4x – 1
Exemplo 3:
Podemos construir uma matriz quadrada com os pontos fornecidos e um ponto genérico (x, y). O determinante dessa matriz será a equação da reta. Observe:
P1(2, 7) e P2(–1, –5)
Aplicando Sarrus: produto dos termos da diagonal principal subtraído do produto dos termos da diagonal secundária.
[(x * 7 * 1) + (–1 * 1 * y) + (–5 * 2 * 1)] – [(–1 * 7 * 1) + (y * 2 * 1) + (–5 * x * 1)] = 0
[7x – y –10] – [–7 + 2y – 5x] = 0
7x – y – 10 + 7 – 2y + 5x = 0
12x – 3y – 3 = 0
–3y = –12x + 3 (dividir todos por – 3)
y = 4x – 1
[7x – y –10] – [–7 + 2y – 5x] = 0
7x – y – 10 + 7 – 2y + 5x = 0
12x – 3y – 3 = 0
–3y = –12x + 3 (dividir todos por – 3)
y = 4x – 1
Retas perpendiculares
Sabemos da Geometria Plana que duas retas são perpendiculares quando são concorrentes e formam entre si um ângulo reto (90º) . Sejam as retas r: y = mr x + nr e s: y = ms x + ns . Nestas condições podemos escrever a seguinte relação entre os seus coeficientes angulares:
ms = - 1 / mr ou mr . ms = -1 .
Dizemos então que se duas retas são perpendiculares, o produto dos seus coeficientes angulares
é igual a -1.
Exemplo:
Dadas as retas de equações (2w - 2)x + (w - 1)y + w = 0 e (w - 3)y + x - 2w = 0, podemos afirmar que:
a) elas são perpendiculares para qualquer valor de w
b) elas são perpendiculares se w = 1
c) elas são perpendiculares se w = -1
d) elas são perpendiculares se w = 0
e) essas retas não podem ser perpendiculares
Solução:
Podemos escrever para a 1ª reta: y = [-(2w-2) / (w-1)].x - w /(w-1).
Analogamente para a 2ª reta: y = [-1 / (w-3)].x + 2w / (w-3). Ora, os coeficientes de x são os coeficientes angulares e, pelo que já sabemos, a condição de perpendicularidade é que o produto desses coeficientes angulares seja igual a -1. Logo:
Efetuando os cálculos indicados e simplificando-se obtemos: w2 - 2w + 1 = 0, que é equivalente a
(w - 1)2 = 0, de onde conclui-se que w = 1.
Mas, cuidado! Observe que 1 anula o denominador da expressão acima e, portanto é uma raiz estranha, já que não existe divisão por zero! Apesar das aparências, a raiz 1 não serve! Logo, a alternativa correta é a letra E e não a letra B como ficou aparente.
Fontes: www.mundoeducacao.com.br
Questões resolvidas sobre equação geral e reduzida da reta e retas perpendiculares
1) Determine a equação reduzida da reta t que forma um ângulo de 135o com o eixo das abscissas e que passa pelo ponto P(4, 5).
Sabemos que α = 135o e que a equação reduzida da reta é da forma y = mx + q. Assim, temos que:
m = tg 135o = – 1
Como a reta t passa pelo ponto P, obtemos:
5 = -1*4 + q
q = 5 + 4 = 9
Portanto, a equação reduzida da reta t é y = – x + 9.
2) Determine a equação reduzida da reta s que passa pelos pontos A(1, 0) e B(3, 4).
m = tg 135o = – 1
Como a reta t passa pelo ponto P, obtemos:
5 = -1*4 + q
q = 5 + 4 = 9
Portanto, a equação reduzida da reta t é y = – x + 9.
2) Determine a equação reduzida da reta s que passa pelos pontos A(1, 0) e B(3, 4).
Solução:
Como conhecemos dois pontos da reta s, podemos encontrar sua equação geral.
Desenvolvendo o determinante obtemos:
2y – 4x + 4 = 0
Isolando y teremos:

Ou
y = 2x – 2
Desenvolvendo o determinante obtemos:
2y – 4x + 4 = 0
Isolando y teremos:
Ou
y = 2x – 2
3) Calcule o coeficiente angular das retas de equações:
a) 3x + 4y - 7 = 0
b) -6x + 8y + 3 = 0
Solução:
a) 4y = -3x + 7
y = -3 x + 7 coeficiente angular = -3
4 4 4
b) 8y = 6x - 3
y = 6 x - 3 = 3 x - 3 coeficiente angular = 3
8 8 4 8 4
4) Ache a equação segmentária da reta de equação geral 2x + 3y - 18 = 0.
Solução:
Podemos escrever: 2x + 3y = 18 ; dividindo ambos os membros por 18 vem:
2x/18 + 3y/18 = 18/18 \ x / 9 + y / 6 = 1.
Vemos, portanto que p = 9 e q = 6 e portanto a reta corta os eixos coordenados nos pontos A(9,0) e B(0,6).
5) Um móvel descreve uma trajetória retilínea e suas coordenadas em função do tempo t , são:
x = 3t + 11y = -6t - 21
Qual a equação segmentária dessa trajetória?
Solução:
Multiplicando ambos os membros da 1ª equação paramétrica por 2, vem: 2x = 6t + 22. Somando agora membro a membro com a 2ª equação, obtemos: 2x + y = 32 (observe que a variável t é eliminada nessa operação pois 6t + ( -6t ) = 0 ). Dividindo ambos os membros da equação obtida por 32 fica:
2x / 32 + y / 32 = 32 / 32 \ x / 16 + y / 32 = 1, que é a equação segmentária procurada.
6) Determine a equação geral da reta sabendo que os pontos A(2,1) e B(- 2,4) pertencem a reta.
Solução:
Com dois pontos podemos determinar a equação da reta:
y = ax + b
*1 = 2a + b
*4 = -2a + b (+)
5 = b
2a + b = 1
2a + 5 = 1
2a = - 4
a = - 2
Logo a equação da reta é y = - 2x + 5, passando para a forma de equação geral fica:
2x + y - 5 = 0
7) A reta r é perpendicular à reta s. Sabendo-se que a reta s possui o seu coeficiente ângular igual à 1/2 e que a reta r passa pelo ponto A(5,3), determine a equação geral da reta r.
Solução:
Para determinarmos a equação geral da reta r, necessitaremos do seu coeficiente ângular e de um ponto. Como as retas r e s são perpendiculares, logo o produto de seus coeficientes é igual à -1.
mr * ms = - 1
mr * (1/2) = - 1
mr = - 2
Reta r : mr = - 2 ; A(5,3)
y - yo = m(x - xo)
y - 3 = - 2(x - 5)
y - 3 = - 2x + 10
y = - 2x + 13
2x + y - 13 = 0
Para determinarmos a equação geral da reta r, necessitaremos do seu coeficiente ângular e de um ponto. Como as retas r e s são perpendiculares, logo o produto de seus coeficientes é igual à -1.
mr * ms = - 1
mr * (1/2) = - 1
mr = - 2
Reta r : mr = - 2 ; A(5,3)
y - yo = m(x - xo)
y - 3 = - 2(x - 5)
y - 3 = - 2x + 10
y = - 2x + 13
2x + y - 13 = 0
8) Determine a equação da reta que passa pelo ponto P (-1, -2) e forma com os eixos coordenados um triângulo de área 4 u.a.
Solução:
Seja m o coeficiente angular da reta:
y - (-2) = m*[x - (-1) -----> y = mx + m - 2
Para x = 0 ----> y = m - 2
Para y = 0 ----> x = - (m - 2)/m
S = x*y ----> S = - [(m - 2)/m]*(m - 2)/2 ----> 4 = - (m - 2)²/2m ----> 8m = - (m - 2)² ----> 8m = - m² + 4m - 4 -----> m² + 4m + 4 = 0
Raiz dupla ----> m = - 2
Reta ----> y = - 2x - 2 - 2 -----> y = - 2x - 4
y - (-2) = m*[x - (-1) -----> y = mx + m - 2
Para x = 0 ----> y = m - 2
Para y = 0 ----> x = - (m - 2)/m
S = x*y ----> S = - [(m - 2)/m]*(m - 2)/2 ----> 4 = - (m - 2)²/2m ----> 8m = - (m - 2)² ----> 8m = - m² + 4m - 4 -----> m² + 4m + 4 = 0
Raiz dupla ----> m = - 2
Reta ----> y = - 2x - 2 - 2 -----> y = - 2x - 4
9) (PUC) Determine a equação da reta com coeficiente angular igual a - 4/5, e que passa pelo ponto p (2, -5).
Solução:
Y = - 4X / 5 + b <~~~~coeficiente angular igual a - 4/5
...que passa em (2,-5)...
-5 = - 4x2 / 5 + b
b = -5 + 8/5
b = (8-25) /5
b = - 17/5 <~~~~
............
Y = - 4X / 5 - 17/5
5Y = - 4X - 17
10) Considere no plano cartesiano uma reta r de equação 3x + 5y +1 =0 e um ponto Q de coordenadas (5,5). Determine a equação da resta s perpendicular a r passando por Q.
Solução:
Solução:
12) Prove que as retas s: x + 2y – 1 = 0 e r: 4x – 2y +12 = 0 são perpendiculares.
Solução:
13) (UFSC) De acordo com o gráfico abaixo, assinale a(s)
proposição(ões) VERDADEIRA(S).
01. A equação da reta s é 3x – 2y + 6 = 0.
02. A reta s e a reta r são perpendiculares.
04. As retas r e s se interceptam no ponto de abscissa 4/5.
08. A área da região do plano limitada pelas retas r, s e pelo eixo das abscissas é igual a 3/10 unidades área.
Solução:
01 – Conforme o gráfico, a reta s intercepta o eixo x no ponto -2, então já temos um ponto, que é (-2,0).
O outro ponto é (0,3), pois é onde a reta corta o eixo y.
Com esses dois pontos fica fácil obter a equação da reta com os dois pontos e um terceiro (x,y) sendo a área desses ponto igual a zero, para que seja uma reta:
|0 -2 x 0| = 0
|3 0 y 3 |
-2y+3x+6 = 0
Preposição verdadeira
02 – Para que as retas sejam perpendiculares, seus coeficientes angulares devem ser opostos e inversos.
Para obter o coeficiente angular, devemos observar a equação reduzida das duas retas, vejamos na reta s:
-2y+3x+6 = 0
2y = 3x+6
y = 3x+3
2
O coeficiente angular será 3/2, o coeficiente de x.
Na reta r devemos encontrar a equação reduzida, sabemos que ela é representada por:
y = ax+b
Sabemos pelo gráfico que quando x é 0 y é 1, portanto:
1 = 0.a+b
b = 1
Portanto:
y = ax+1
Quando y = 0, x = 1. Logo:
0 = a.1+1
a = -1
Como a é -1, esse é o coeficiente angular da reta.
Com -1 e 3/2 não temos oposto nem inverso.
Ítem falso
04 – Para que as retas interceptem-se no ponto x=4/5, lembra que abscissa é x, abXissa, aplicando esse ponto em x na equação reduzida das retas, y deve ter o mesmo valor nas duas:
Reta s
y = 3x+3
2
y = 3. 4 + 3
2 5
y = 12 + 1
10
y = 22
10
y = 11
5
Reta r
y = -x+1
y = -4 + 1
5
y = 1
5
Ítem falso
08 – Será a área por coordenadas entre os pontos (-2, 0); (1,0) e o ponto de intersecção das duas retas, que é o ponto comum entre as duas, para achar esse ponto, resolvemos as duas equações de reta como um sistema linear, achando x e y que é comum aos dois:
y = 3x+3 y = -x+1
2
y = -x+1
Substituindo y pelo seu valor na primeira reta:
3x+3 = -x+1
2
-2x+2 = 3x+3
5x = 1
x = 1/5
y = -x+1
y = -1+1
5
y = 4/5
O ponto é (1/5, 4/5) e a área será:
A = 1/2|-2 1 1/5 -2|
| 0 0 4/5 0|
A = 1/2 |4/5+8/5|
A = 1/2. 12/5
A = 12/10
A = 6/5
Falso
Soma dos ítens verdadeiros: 01
14) (UDESC 2008) A soma do coeficiente angular com o coeficiente linear da reta que passa pelos pontos A(1, 5) e B(4, 14) é:
a) 4
b) -5
c) 3
d) 2
e) 5
15) (ADVISE 2009) A equação geral da reta tangente à curva y = x² + x no ponto de abscissa 1 é:
a) 3x – y – 1 = 0
b) 3x – y = 0
c) 2x – y – 1 = 0
d) 2x – y = 0
e) 5x – 2y – 2 = 0
16) (USP) A equação da reta perpendicular ao eixo das abscissas que passa pelo ponto médio do segmento AB, onde A(2, 3) e B é o centro da circunferência de equação x2 + y2 - 8x - 6y + 24 = 0, é:
a) y = 3
b) y = 4
c) x = 4
d) x = 3
e) 3x + 4y = 0
17) Determinar as equações das retas (t) tangentes à circunferência x² + y² + 2x - 3 = 0 e que passam pelo ponto P(5, 2). Resp: y - 2 = 0 e 3x - 4y - 7 = 0
Muito bom!!!!!
ResponderExcluirOi pode me ajudar ? AS RETAS(r) 2x+3y-8=0 e (s) -2x+4x-13=0 sao concorrentes num ponto M . Determine as coordenadorcoordenadas do ponto M
ResponderExcluir